STRUKTUR DATA GRAPH

 

Struktur Data Graph: Pengertian, Jenis, dan Kegunaannya

Struktur data menyediakan cara dalam menyimpan data agar dapat dikelola dengan mudah, ditangani secara efektif, serta tertata dengan baik. 

Adanya berbagai jenis struktur data bertujuan untuk mengelola beberapa jenis data yang berbeda. Biasanya ada data yang perlu penanganan khusus yang tidak dapat disimpan dalam format sederhana.

Kita sebagai seorang yang bergelut di bidang IT dituntut agar memahami berbagai jenis struktur data agar dapat memilih struktur data yang tepat sesuai dengan kasus yang dihadapi.

Nah, di kesempatan ini, kita akan belajar salah satu struktur data yang tak kalah penting, yaitu 

Pengertian Graph

Graph adalah jenis struktur data umum yang susunan datanya tidak berdekatan satu sama lain (non-linier). Graph terdiri dari kumpulan simpul berhingga untuk menyimpan data dan antara dua buah simpul terdapat hubungan saling keterkaitan.

Simpul pada graph disebut dengan verteks (V), sedangkan sisi yang menghubungkan antar verteks disebut edge (E). Pasangan (x,y) disebut sebagai edge, yang menyatakan bahwa simpul x terhubung ke simpul y.

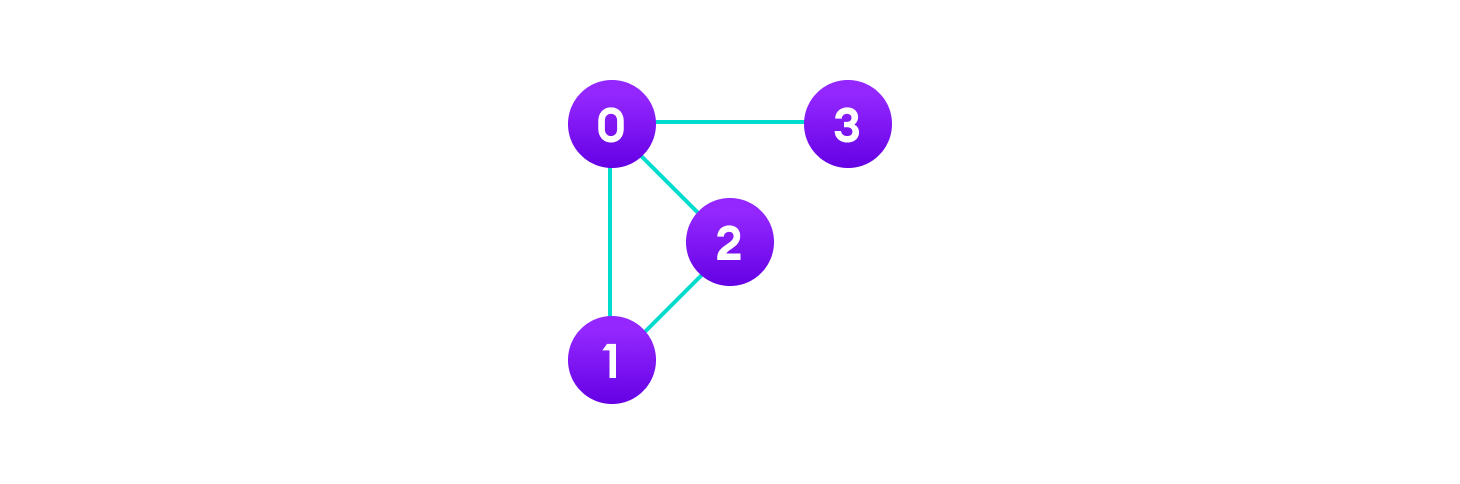
Sebagai contoh, terdapat graph seperti berikut:

Sumber: programiz.com

Graph di atas terdiri atas 4 buah verteks dan 4 pasang sisi atau edge. Dengan verteks disimbolkan sebagai V, edge dilambangkan E, dan graph disimbolkan G, ilustrasi di atas dapat ditulis dalam notasi berikut:

V = {0, 1, 2, 3}

E = {(0,1), (0,2), (0,3), (1,2)}

G = {V, E}

Graph banyak dimanfaatkan untuk menyelesaikan masalah dalam kehidupan nyata, dimana masalah tersebut perlu direpresentasikan atau diimajinasikan seperti sebuah jaringan. Contohnya adalah jejaring sosial (seperti Facebook, Instagram, LinkedIn, dkk)

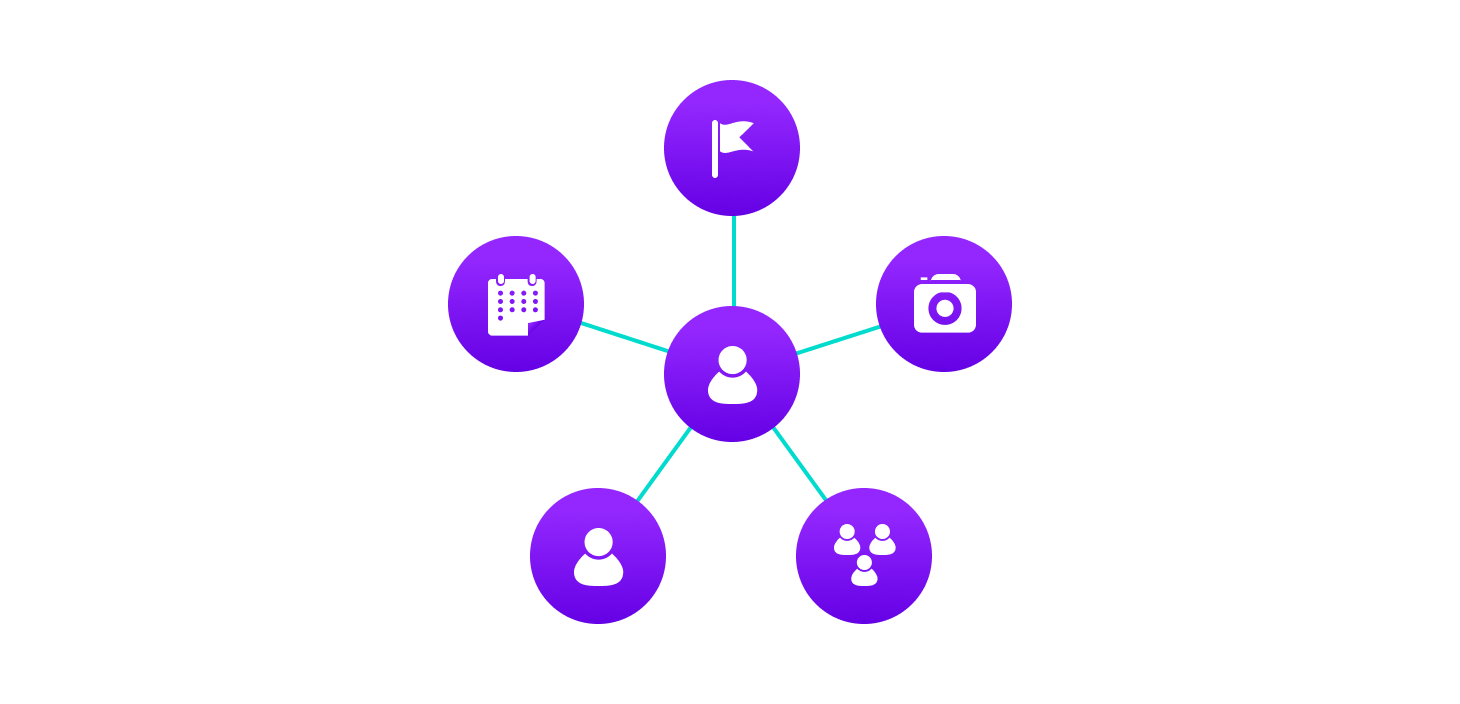
Pengguna di Facebook dapat dimisalkan sebagai sebuah simpul atau verteks, sementara hubungan pertemanan antara pengguna tersebut dengan pengguna lain direpresentasikan sebagai edge. Tiap tiap verteks dapat berupa struktur yang mengandung informasi seperti id user, nama, gender, dll.

Tidak hanya data pengguna, data apapun yang ada di Facebook adalah sebuah simpul atau verteks.Termasuk foto, album, komentar, event, group, story, dll. 

Pengguna dapat mengunggah foto. Ketika telah diunggah, foto akan menjadi bagian dari album. Foto juga dapat dikomentari oleh pengguna lain dan mereka dapat saling berbalas komentar.

Semuanya terhubung satu sama lain, baik dalam bentuk relasi one-to-many, many-to-one, atau many-to-many.

Sumber: programiz.com

Jenis-jenis Graph

Graph dapat dibedakan berdasarkan arah jelajahnya dan ada tidaknya label bobot pada relasinya.

Berdasarkan arah jelajahnya graph dibagi menjadi Undirected graph dan Directed graph.

Undirected Graph

Pada undirected graph, simpul-simpulnya terhubung dengan edge yang sifatnya dua arah. Misalnya kita punya simpul 1 dan 2 yang saling terhubung, kita bisa menjelajah dari simpul 1 ke simpul 2, begitu juga sebaliknya.

Sumber: educative.io

Directed Graph

Kebalikan dari undirected graph, pada graph jenis ini simpul-simpulnya terhubung oleh edge yang hanya bisa melakukan jelajah satu arah pada simpul yang ditunjuk. Sebagai contoh jika ada simpul A yang terhubung ke simpul B, namun arah panahnya menuju simpul B, maka kita hanya bisa melakukan jelajah (traversing) dari simpul A ke simpul B, dan tidak berlaku sebaliknya.

Sumber: educative.io

Selain arah jelajahnya, graph dapat dibagi menjadi 2 berdasarkan ada tidaknya label bobot pada koneksinya, yaitu weighted graph dan unweighted graph.

Weighted Graph

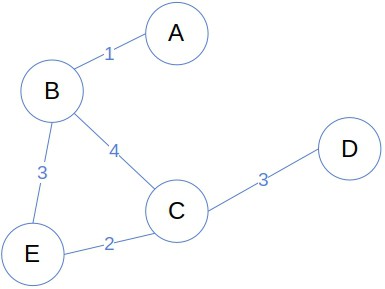
Weighted graph adalah jenis graph yang cabangnya diberi label bobot berupa bilangan numerik. Pemberian label bobot pada edge biasanya digunakan untuk memudahkan algoritma dalam menyelesaikan masalah.

Contoh implementasinya misalkan kita ingin menyelesaikan masalah dalam mencari rute terpendek dari lokasi A ke lokasi D, namun kita juga dituntut untuk mempertimbangkan kepadatan lalu lintas, panjang jalan dll. Untuk masalah seperti ini, kita bisa mengasosiasikan sebuah edge e dengan bobot w(e) berupa bilangan ril.

Sumber: baeldung.com

Nilai bobot ini bisa apa saja yang relevan untuk masalah yang dihadapi: misalnya jarak, kepadatan, durasi, biaya, probabilitas, dan sebagainya.